Taoffi's blog

Numeral systems are fascinating!

Presenting values in various numeral systems reveals some hidden aspects of these values and sometimes reveals more about our Human History and knowledge evolution.

Roman is one of these systems. (you may have a look here, here, or here)

A few years ago, I wrote a method to convert decimal numbers into roman. That worked well. The customer wanted a converter for numbering paragraphs. Up to 50 would be largely enough, he said. The developer in my head pushed me up to 9999 (sadly, I abandoned here by lack of time)

A few days ago, I saw someone wearing a T-shirt with 'XCIV' logo. And that reminded me that I never wrote the reverse conversion (from roman to decimal).

That was a good occasion to write this. And as I also have a friend who wants to practice C#, that may be a good exercise.

I found back my old code (to discover it was all to be rewritten!)… and I started working on a new version!

Roman numerals. A brief presentation

As you may know, Roman numerals building blocks are:

Intermediate values (like in the table below, between 1 and 10) are additions and subtractions of these basic building blocks

Going beyond the M (1000) [presentation and entries]

Roman numerals were, at their era, (an evidence) hand written (probably more often engraved on hard stones!).

That surely does not mean the people did not know or need to count beyond the 1000. We better never forget that numbers and mathematics are much older than our own era… and that most of the great advances in this area had been achieved in other older civilizations!.

My problem here is just a presentation question: how can I write roman numbers beyond the M (1000)?

Old traditionalists use quirky figures that do not seem easily writable using a 'keyboard'.

Like here:

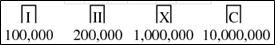
Or here:

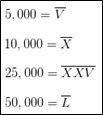
To make presentation and entries a little easier with our era's keyboards, I decided to combine other units to create building blocks beyond the 1000. Example: To present the 1000 – 9000 sequence, I used 'XM' and 'VXM':

For the sequence 1m – 9m, I used characters that are not in the traditional roman building blocks: The 'U', 'W' and 'Y':

Conversion processing units

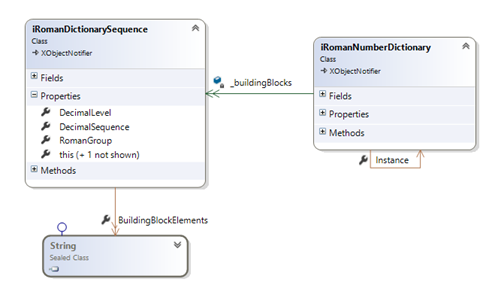
The conversion manager object (iRomanNumberDictionary in the above figure) stores a list of roman building blocks.

Each building block corresponds to a decimal sequence factor (1, 10, 100, 1000… etc.) and stores the roman elements of this sequence (see the sample tables above). It also stores the roman group level (a vital info as you will see in the code!)

Decimal to roman

Now, to convert a decimal number into its roman presentation, we proceed this way (here, using 28 as an example):

• Take the leftmost digit of the number (leftmost of 28 = 2)
• Set the index of the sequence to look in = count of number's digits - 1 (for 28 that is 2 – 1 = 1)
  • Note: this target sequence is composed of: "X", "XX", "XXX", … etc.
• Find the value of this sequence at the element index = the leftmost digit – 1 (2 – 1 = 1)
• In our case, that would be "XX" (which is decimal 20)
• Recurse call with the remaining digits of the number (remaining of "28" = "8")
  • Note: that call should return "VIII" (first sequence at the 7^th position)
• Add the string to the "XX" (that would then be "XXVIII")

Roman to decimal

Roman to decimal is a bit trickier!

Let us take the reverse conversion of the example above ("XXVIII") for which the conversion result should be 28.

• The conversion step (a parameter) should be set to the highest index of our roman sequences (in my app, I used 7 sequence groups whose factors are: 1, 10, 100, 1000, 10000… 1000000)
• We have to look for the string in all sequences whose group order is <= the current step
• Do until we find something:
  • In our example: we look for "XXVIII" in all sequences whose group order is <= 7
  • As the string is not found in any sequence, we continue the search using the string minus 1 char "XXVII"… "XXVI"… "XXV"… "XX"
  • "XX" is found in the sequence whose decimal factor = 10 at number zero-index = 1
  • We store the following value in a List<int>: sequence's decimal factor * (number zero-index + 1). Which results in 10 * 2 = 20
• Recurse call using the remaining string "VIII" and using the sequence group order – 1 as the conversion step. Add the returned number to our List<int>
• Return the sum of integers of our List<int>

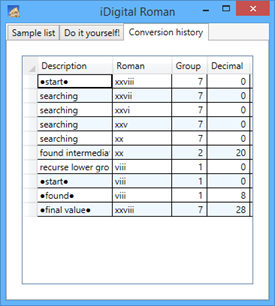
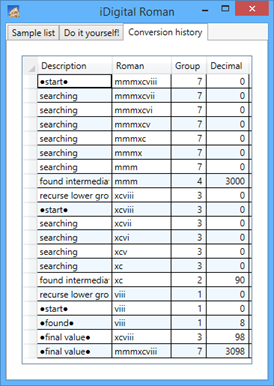
To better understand what goes on in the conversion process, I added a conversion history that explains the steps of each conversion.

Here is the processing history for XXVIII (28):

Another processing history for a greater roman number MMMXCVIII (3098):

You may download the code (WPF) HERE. Have fun extending and enhancing for the better!